【効率的な条件探索】Multi-Sigmaで簡単ベイズ最適化

2025年1月31日

緻密な最適化

皆さんは、こんな経験はありませんか？

「売上予測を立てたものの、その予測がどのくらい確かなものなのか分からない…」「製品の最適な製造条件を見つけたいが、実験回数は限られている…」

そんな時に役立つのが、「ガウス過程回帰」であり、それに獲得関数というものを組み合わせた「ベイズ最適化」です。

予測の「確かさ」を知る重要性

予測には必ず「不確実性」が伴います。多くの予測手法は単一の予測線のみを提供しますが、ガウス過程回帰では、予測値に加えて、その予測の不確実性の範囲も示すことができます。この「不確実性」を知ることは、ビジネスや研究開発において非常に重要な意味を持ちます。

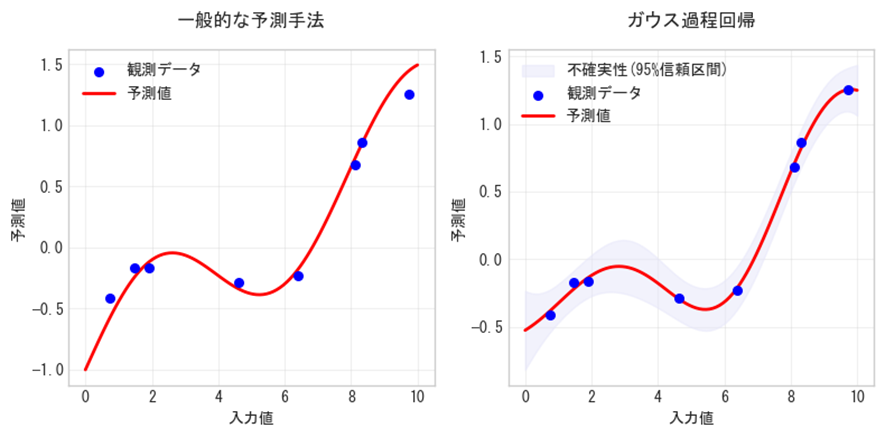
図１：ガウス過程回帰による予測

予測の不確実性を把握することで、私たちの意思決定は大きく変わります。例えば、ある製造条件での品質予測において、「品質スコアは85点になる」という予測だけでなく、「85±3点の範囲に収まる可能性が高い」という情報があれば、より現実的な計画立案が可能になります。リスクの定量的な評価ができることで、最悪のケースも想定した計画が立てられ、予算や資源の適切な配分も実現できるのです。

また、不確実性の高い領域を特定できることは、リスク管理の観点からも重要です。重点的な監視が必要な箇所を把握し、予防的な対策を実施することができます。さらに、データに基づく客観的な判断が可能になることで、意思決定の質も向上します。複数のシナリオを検討しやすくなり、より説得力のある説明も可能になるのです。

従来の予測手法との違い

ガウス過程回帰の特徴を理解するために、他の予測手法と比較してみましょう。

線形回帰や多項式回帰では多くの場合、データの傾向を直線や単純な曲線で表現するため、複雑な関係性を捉えることが困難でした。一方、ガウス過程回帰は、複雑な非線形関係も柔軟に表現することができます。

ニューラルネットワークは、確かに高度な予測が可能ですが、そのためには大量のデータが必要です。これに対してガウス過程回帰は、比較的少ないデータでも効果的に機能します。新製品の開発初期段階や、高コストな実験データを扱う場合には、この特徴が大きな強みとなります。

予測の「確かさ」を数値で把握する

製品開発や実験計画の現場では、「次にどうなるか」を予測することが重要です。しかし、単なる予測値だけでは不十分です。その予測がどの程度信頼できるのか、という情報も同じく重要なのです。

ガウス過程回帰は、まさにこの「予測の確かさ」を定量的に示してくれます。例えば、ある製品の品質予測において「品質スコアは85±3点の範囲に収まる確率が95%」といった具体的な指標が得られます。また、新しい製造条件を検討する際には、「この条件での収率は70%を超える可能性が80%以上」といった形で、不確実性を含めた予測が可能です。

データ量による手法の使い分け

予測手法の選択において、扱うデータ量は重要な判断基準となります。ニューラルネットワークは、大量のデータが利用可能な場合に真価を発揮します。

一方、ガウス過程回帰は、数十件程度の比較的少ないデータでも効果的に機能します。特に、予測の不確実性の評価が重要な場面や、実験計画の最適化が必要な場合に役立ちます。高コストな実験データを扱う研究開発の現場では、この特徴が大きな価値を持つでしょう。

カーネルの種類と特徴

ガウス過程回帰において、データの特徴を捉えるための重要な要素が「カーネル」です。カーネルは、データの中にある特徴やパターンを見つけ出すための「レンズ」のような役割を果たします。異なるカーネルを選択することで、データの異なる特徴（滑らかさ、周期性など）を捉えることができます。

●RBF（Radial Basis Function）カーネル

最も汎用的なカーネルとして知られるRBFカーネルは、無限回微分可能な滑らかな関数を生成します。温度と反応速度の関係や、圧力と変形量の関係など、多くの自然現象の分析に適しています。データの変化が連続的で緩やかな場合に、優れた予測性能を発揮します。

●Matérn 3/2カーネル

1回微分可能な関数を生成するカーネルです。RBFカーネルよりも急激な変化を許容し、データにある程度の不連続性がある場合にも対応できます。気象データの分析や、地理空間データの補間など、完全には滑らかでない現象のモデル化に適しています。

●Matérn 5/2カーネル

2回微分可能な関数を生成し、Matérn 3/2とRBFの中間的な特徴を持ちます。材料特性の予測や、生産プロセスの最適化など、幅広い応用場面で活用されています。

●Periodicカーネル

周期的なパターンを持つデータの分析に特化したカーネルです。季節性のある売上データや周期的な設備の振動データ、日周期の需要変動など、繰り返しパターンを持つデータの予測に適しています。周期の長さを明示的に指定できる点が特徴です。

●Linearカーネル

線形的な傾向を持つデータに適したカーネルです。経済指標の推移や技術の進歩による性能向上、累積的な効果の分析など、単調な増加や減少を示すデータの予測に効果的です。長期的なトレンドの把握に優れています。

●Exponentialカーネル

データの非連続な変化や急激な変動を表現するのに適したカーネルです。物理的な相転移や、社会システムでの急激な変化など、滑らかではない現象のモデル化に効果を発揮します。

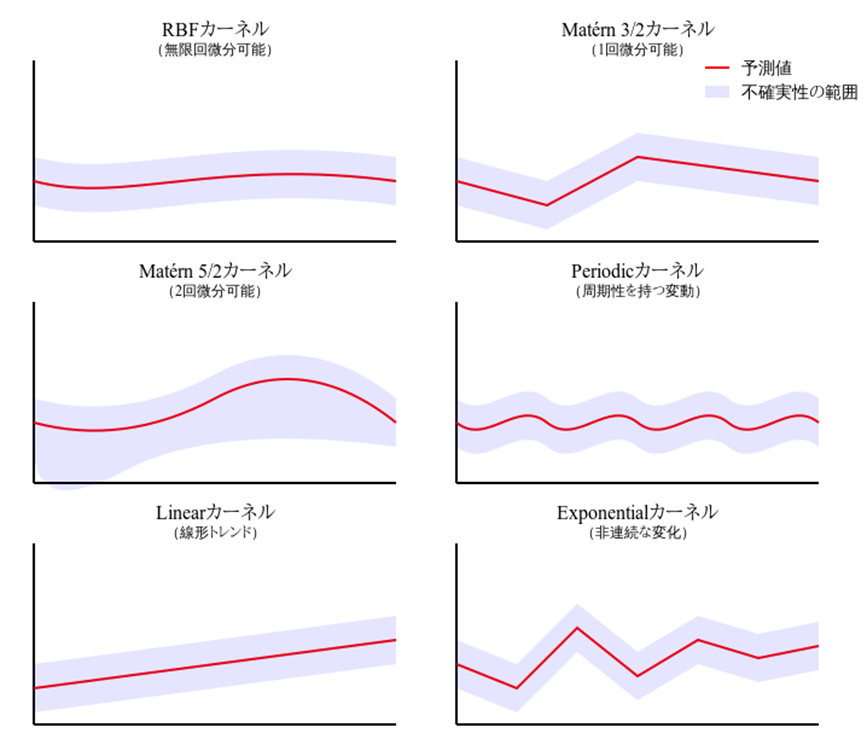
図２：それぞれのカーネルのイメージ

カーネルパラメータの役割

各カーネルには、データの特徴を捉えるためのパラメータが存在します。

●Lengthscale

データの変化の特徴的な長さを制御するパラメータです。小さな値を設定すると、データの細かい変動を捉えることができます。逆に大きな値を設定すると、全体的なトレンドを重視した滑らかな予測となります。

●Variance

予測値の全体的なばらつきの大きさを制御します。大きな値を設定すると予測の不確実性も大きくなり、小さな値では予測がより確定的になります。

●Period

Periodicカーネルでのみ使用します。データの周期を表現するパラメータです。

●Gaussian Noise Variance

観測データに含まれるノイズの大きさを表現するパラメータです。データにノイズが多い場合は大きな値を、高精度なデータの場合は小さな値を設定します。

Multi-Sigmaでのガウス過程回帰

Multi-Sigmaでは、カーネルの種類を指定してガウス過程回帰を行うことが可能です。個々のパラメータの値を指定することも可能ですが、これらのパラメータの自動調整機能が実装されています。ユーザーは、カーネルの種類を選択するだけで、高精度な予測モデルを構築することができます。各パラメータは入力データの正規化後のスケールで適用されます。

ベイズ最適化への応用

これまで、ガウス過程回帰の基本的な考え方とカーネルの特徴について見てきました。次は、この手法を最適化問題に応用する「ベイズ最適化」について解説していきます。

効率的な最適化への挑戦

実験や開発のプロセスでは、「限られた試行回数で最適な条件を見つけたい」というニーズが常にあります。従来の最適化手法では、考えられる全ての条件を網羅的に試すか、経験則に基づいて条件を選んでいました。しかし、ベイズ最適化では、これまでの実験結果を学習しながら、次に試すべき条件を賢く選択します。

この「賢い選択」を可能にするのが、ガウス過程回帰による予測と不確実性の評価です。予測値だけでなく、その不確実性も考慮することで、より効率的な探索が可能になります。

獲得関数の役割

ベイズ最適化において、次の実験条件を決定する際の指針となるのがEIやPIといった「獲得関数」です。獲得関数は、予測値と不確実性のバランスを考慮しながら、最も有望な条件を提案します。

●改善期待値（EI）

最も広く使われている獲得関数が、Expected Improvement（EI）です。この関数は、現在の最良値からどれだけ改善が期待できるかを数値化します。未開拓の条件域に大きな可能性を見出し、チャレンジングな選択をします。もちろん、その予測には不確実性が伴いますが、大きな改善のチャンスを逃さないよう、敢えてそのような条件を選ぶのです。

●改善確率（PI）

より確実な改善を重視する場合には、Probability of Improvement（PI）が適しています。この関数は、現在の最良値を上回る確率を直接評価します。予測の不確実性が小さい領域で、かつ予測値が現在の最良値に近い場合に高い値を示します。劇的な改善は期待できないものの、着実に性能を向上させたい場合、特に量産工程の改善などでは、この安全策が有効です。

●平均（Mean）

この方法は、ガウス過程回帰による予測の平均値のみを考慮し、不確実性は考慮しません。探索空間において、純粋に予測値が最も高い地点を次の評価点として選択します。

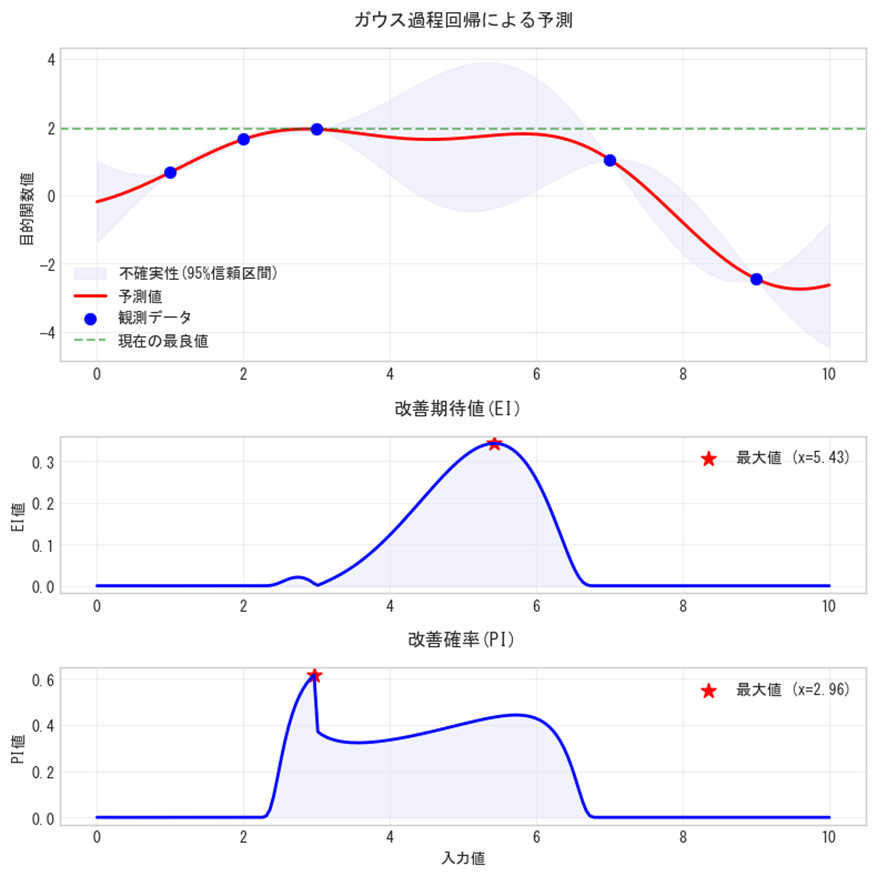
図３：獲得関数

Multi-Sigmaでのベイズ最適化

Multi-Sigmaでは、これらの複雑な処理を簡単な操作で実行できます。最適化の目的と制約条件を設定するだけで、ベイズ最適化による効率的な条件探索が始まります。

特に重要なのは、複数の目的関数を同時に考慮できる点です。例えば、材料開発では「強度を最大化」しながら「コストを最小化」するといった、相反する要求のバランスを取る必要があります。Multi-Sigmaでは、これらの要求を重み付けして評価することで、実用的な最適解を見つけることができます。

また、実験の制約条件も柔軟に設定できます。温度や圧力の上限、原料の配合比の制約など、現実の製造プロセスで考慮すべき様々な条件を組み込むことができます。

データ駆動の意思決定へ向けて

ガウス過程回帰とベイズ最適化の導入は、単なる効率化以上の価値をもたらします。予測の不確実性を定量的に評価できることで、より戦略的な意思決定が可能になります。また、データに基づく客観的な判断は、組織の意思決定プロセスの透明性と説明責任の向上にも貢献します。