実験条件、まだ「勘」で決めていませんか？AI解析の成果を最大化する、スマートなデータ準備術

金曜の夕方、あなたはエクセルとにらめっこしていませんか？

新しい材料の配合比率。製造プロセスにおける温度と圧力。反応時間と触媒の量—。
来週の実験条件を決めるため、エクセルのセルに数字を並べながら、こんなことを考えていませんか？
「これまでの経験則で、だいたいこの辺りを試せばいいか…」
「とりあえず、最小値と最大値の間を等間隔で振ってみよう」
「前回うまくいった条件の近くを、もう少し細かく…」

その作業、実は研究開発のスピードを大きく左右する、最も重要な判断なのです。
にもかかわらず、多くの現場では「勘」と「手作業」に頼っているのが現実。もしあなたがそうなら、決して恥ずかしいことではありません。むしろ、ほとんどの技術者が同じ悩みを抱えています。

でも、もう少しだけ立ち止まって考えてみてください。
もしその実験計画に「見えないムダ」があったとしたら？
そして、それを数クリックで解決できる方法があるとしたら？
この記事ではその解決策をご紹介します。

AIは「学習するデータ」で9割が決まる

「うちもAIを活用して、開発スピードを上げたい」
そう考えて、いざAI解析を始めようとしたとき、多くの方がぶつかる壁があります。
それは、「AIに学習させるための、良質なデータがそもそも作れない」という問題です。

実は、AIの予測精度を決めるのは学習アルゴリズムだけではありません。どんな実験データを食べさせるかが、決定的に重要です。
どれだけ優れた学習アルゴリズムを使用しても、学習データに「偏り」や「ムラ」があれば、精度の高いモデルは生まれません。

人間が決めると、どうしても「バイアス」がかかる

人間が実験条件を決めると、どうしても無意識のバイアスが入り込みます。

• 安全志向のバイアス：失敗したくない心理から、「安全圏」の条件ばかりを選んでしまう
• 経験依存のバイアス：過去にうまくいった条件の周辺ばかりを探索してしまう
• 空白地帯の放置：「たぶん結果が悪そう」と思う領域を、無意識に避けてしまう

その結果、データは特定の領域に集中し、他の領域はスカスカのまま。こうなると、AIはその空白地帯について何も学べません。

一方で逆方向の落とし穴もあります

「実験条件の穴を作りたくない」「実験回数は多ければ多いほどよい」という心理から、実験条件を必要以上に増やしてしまうバイアスも存在します。

• 網羅志向のバイアス：可能な限り多くの実験を実施すればAIモデルが完璧になると思い、必要以上に実験条件を設定してしまう
• 解像度過剰のバイアス：細かく設定することでほとんど同じ条件を大量に増やし、情報としては増えていないデータを積み上げてしまう

その結果、データ数は多いのに新しい学びが少ない状態になり、本来データ分析や考察のために使用できた時間をデータ収集のために費やしてしまい、研究の質を高めることができません。
大切なことはむやみやたらに実験回数を増やすことではなく、少ない実験でどれだけ新しい情報を得るかです。
つまり、「どんな実験をするか」を決める段階で、すでに勝負は9割決まっているのです。

解決策：実験計画を「科学的」に、しかも「自動」で作る

「でも、実験計画法って難しそうだし、時間もないし…」
そう思われた方、ご安心ください。
私たちのAI解析ツール「Multi-Sigma®」には、解析機能だけでなく、実験計画の自動作成機能が標準搭載されています。
難しい統計の知識は一切不要。ブラウザ上で簡単な設定を入力するだけで、AIが学習しやすい、バランスの取れた実験条件リストを自動生成します。
しかも、あなたの研究開発の段階に応じて、2つの強力な手法を使い分けることができます。

【第一段階】まずは全体像を掴む：「ラテン超方格法（LHS）」

新しいテーマに取り組むとき、最初にぶつかる問題はこれです。
「パラメータの範囲が広すぎて、どこから手をつければいいかわからない…」
そんなとき、役立つのが「ラテン超方格法（LHS：Latin Hypercube Sampling）」です。

数独（ナンプレ）のように、空間全体に点を配置する

この手法は、いわば「多次元の数独」です。
数独では、縦の列にも横の行にも、1〜9の数字が重複しないように配置しますよね。ラテン超方格法も同じ原理で、パラメータ空間全体にまんべんなく、重ならないように実験点を散りばめます。

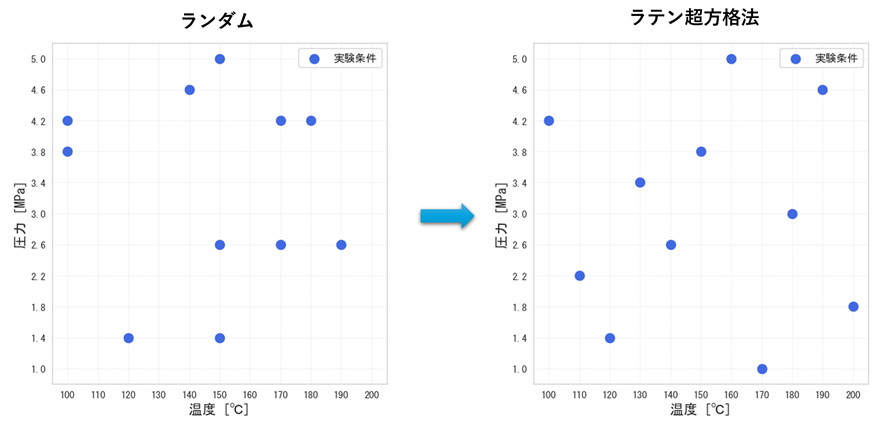
なぜランダムよりも優れているのか？

たとえば、温度と圧力という2つのパラメータで実験するとします。

ランダムに選ぶと：
運が悪ければ、同じ温度や同じ圧力に実験条件が集中してしまい、せっかく10回実験しても探索できる範囲が偏ります。

ラテン超方格法で選ぶと：
各パラメータの全範囲が必ずカバーされます。少ない実験回数で、広い空間の傾向を効率的に把握できます。

Multi-Sigma®での使い方はシンプル

1. CSVファイルを選択（既存データがあれば読み込み、なければ不要）
2. 生成オプションで「ラテン超方格法」を選択
3. 生成したいデータ数（実験回数）を入力
4. 各パラメータの最小値・最大値・刻み幅を設定
5. ボタンをクリック
   これだけで、最適化された実験条件リストが完成します。

【第二段階】精度を極める：新機能「空間充填法」

ラテン超方格法を使って効率よく初期データを収集し、AIモデルの構築も順調に進んだ。
全体像が見えてくると、次に湧いてくるのは「このモデルを、さらに高精度に磨き上げたい」という欲求ではないでしょうか。

追加実験の「場所選び」、悩んでいませんか？

精度を上げるために実験データを追加するとき、人間が頭で考えると、どうしても「前回うまくいった条件」の近くを選んでしまいがちです。
しかし、AIの視点で見ると、それは少しもったいないことかもしれません。
　　• 情報の重複：似たような場所ばかり測定しても、AIの知識はあまり増えない
　　• 未知の放置：本当に情報が足りていない「空白地帯」が放置されたままになる
これでは、実験回数を増やしても、労力に見合った精度の向上は望めません。

空間充填法が解決する「隙間の問題」

そこで、Multi-Sigma®に新しく追加された機能が「空間充填法」です。
これは、「今あるデータ」を考慮して、「次にどこを実験すれば一番賢いか」を提案してくれる機能です。

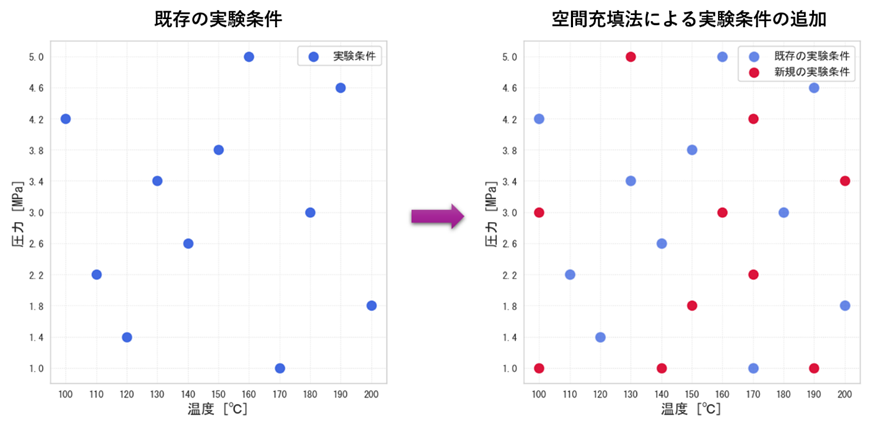
仕組みはこうです：

1. 既存データの位置を認識：システムが、これまでの実験点がパラメータ空間のどこに位置しているかを把握
2. 「隙間」を自動検出：まだ実験していない空白エリアを特定
3. 最も価値の高い点を提案：既存の点からできるだけ離れた、情報価値の高い条件を自動生成

つまり、実験を重ねるごとに、AIの知識の穴が効率よく埋まっていくのです。

「過去のデータ」も、立派な財産です

Multi-Sigma®の空間充填法は、「手持ちの過去データ」の続きからスタートすることができます。

たとえば、過去に直行表で取得したデータをCSVで読み込ませてください。
直行表は人間にとって分かりやすい優れた手法ですが、AIの視点で見ると、どうしてもデータ間に「隙間」が存在します。Multi-Sigma®は、その「直行表の隙間」だけをピンポイントで見つけ出し、「ここさえ追加実験してくれれば、予測精度が劇的に上がります」という条件を提案します。

過去の資産を活かしつつ、最小限の追加実験で最新のAI活用へと橋渡しをする。これも空間充填法の大きなメリットです。

「ベイズ最適化」だけが正解じゃない？現場が抱える”逐次実験”の悩み

AIを使った実験計画といえば、「ベイズ最適化」を思い浮かべる方も多いかもしれません。
ベイズ最適化は、「次に一番可能性が高い点（最適解）」をピンポイントで予測してくれる非常に強力な手法です。

しかし、近年の実験現場では、このアプローチが合わないケースも増えています。

課題：ハイスループット実験との相性
ベイズ最適化は基本的に「1回実験 → 結果入力 → 次の1点を予測 → 1回実験…」というサイクルを繰り返すことを前提としています。
しかし、最近のハイスループット実験（HTE）のように「一度に100通りの実験をロボットに仕込みたい」「マシンの稼働効率を考えて、まとめて実験したい」という現場では、この「ちょこちょこ繰り返す逐次ループ」が大きなボトルネックになります。

解決策：空間充填法による「一括」提案
一方で、Multi-Sigma®の空間充填法は、「次の実験候補を50個、空間全体からバランスよく選んで」といった一括指示が可能です。
これにより、実験機をフル稼働させ、一気にデータを取得することができます。

サロゲートモデル（デジタルツイン）の構築にも最適

また、ベイズ最適化は「特定の正解（ピーク）」を探すことに特化しているため、それ以外の領域のデータがスカスカになりがちです。
対して空間充填法は、実験空間全体の「地図」を高解像度で作ることを目的としています。これにより、実験していない条件でも高精度にシミュレーションできる「サロゲートモデル」を構築したい場合には、空間充填法の方が圧倒的に有利に働きます。

【検証】 従来手法 vs Multi-Sigma® 予測精度の比較

「理屈はわかったけれど、本当に自動生成で精度が上がるの？」
そう疑問に思われる方のために、検証を行いました。

今回は効果を客観的に測定するため、複雑な材料特性を模した「人工モデル（4次元の非線形ベンチマーク関数）」を使用し、シミュレーションを行っています。
実際の実験と同じように観測ノイズ（実験誤差）が含まれる条件下で、AIに学習・予測させた場合の精度比較がこちらです。

縦軸は予測誤差（RMSE）を表しており、棒グラフが低いほど、AIが正確に予測できていることを示します。

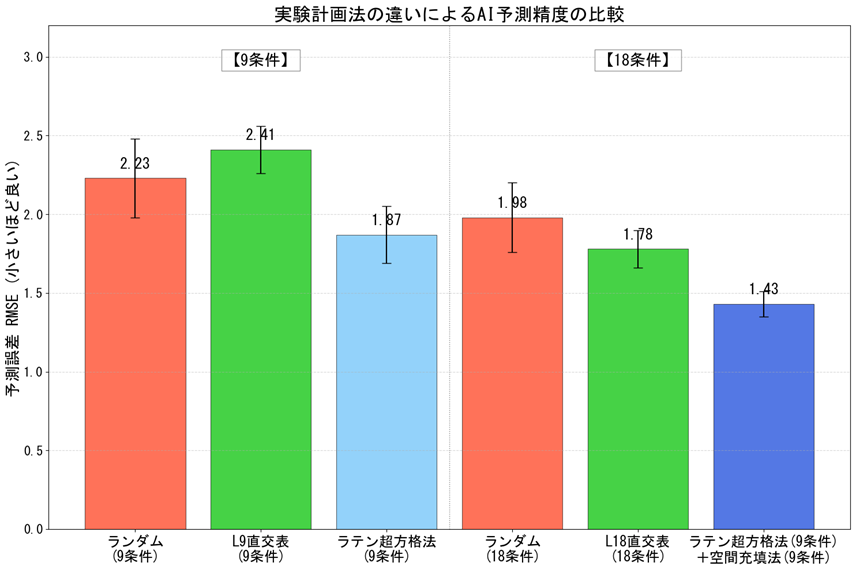
このグラフから分かる3つの真実

1. 直交表は万能ではない（左の緑色のバー）
   「L9直交表」の結果をご覧ください。意外なことに、ランダムよりも予測精度が悪くなっています。
   直交表は人間が要因分析をするには優れた手法ですが、データが等間隔すぎて空間に「死角」ができやすく、AIが複雑な挙動（非線形性）を学習する際には、かえって足かせになることがあります。

2. 「ラテン超方格法」の効率の良さ（中央の水色のバー）
   同じ9条件でも、LHS（ラテン超方格法）を用いるだけで、誤差が下がっています。
   「ランダムの柔軟さ」と「直交表のバランス」をいいとこ取りしたLHSが、いかに少ない実験数で全体像を捉えているかが分かります。

3. 「追加実験」で圧倒的な差がつく（右端の青色のバー）
   データ数を18条件に増やした結果を見てみましょう。
   単にランダムや直交表で数を増やすよりも、「LHSで全体を把握し、空間充填法で弱点を補強する（右端の青バー）」手法が高い精度（低い誤差）を叩き出しています。
   やみくもに実験数を増やすのではなく、「AIが欲しいデータ」をピンポイントで与えることが最短ルートであることを表しています。

「実験順序」も、現場の都合に合わせて最適化

素晴らしい実験計画（レシピ）ができても、実際に実験する現場には「都合」がありますよね。
「温度を変えるのは待ち時間が長いから、できるだけまとめてやりたい」
「まずは材料Aを使う条件を全部終わらせてから、材料Bに移りたい」
数学的に最適化されたリストでも、実験順序がバラバラだと、現場では結局エクセルで並べ替える手間が発生してしまいます。
「理論上は完璧だけど、現場では使いにくい」
これでは本末転倒です。

Multi-Sigma®は「実験のしやすさ」まで考えた

そこでMulti-Sigma®は、出力するCSVデータの「ソート（並べ替え）」機能にもこだわりました。
条件生成の際、各変数に対して以下の設定が可能です：
　　• 優先順位：どの変数を優先して並べ替えるか（例：温度を最優先、次に圧力…）
　　• ソート方向：昇順（小さい順）、降順（大きい順）

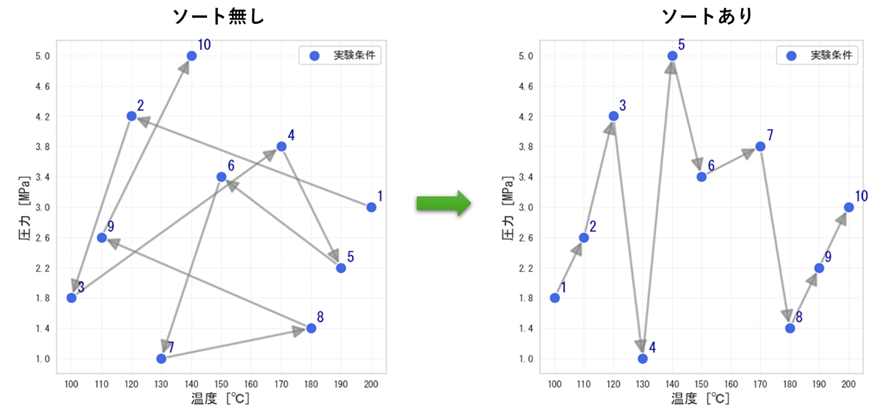
実際の使用例

ケース1：装置の待ち時間と負荷を減らしたい
• 設定：「温度」を優先順位1（昇順）、「圧力」を優先順位2（降順）に設定
• リスト：全体が「低温 → 高温」の流れになり、同じ温度の中では「高圧 → 低圧」順に並ぶ
• メリット：「昇温・降温の待ち時間を大幅に短縮し、圧力調整の工数も削減」

ケース2：材料切り替えの手間を減らしたい
• 設定：「材料種類」を優先順位1（昇順）に設定
• リスト：材料Aの実験をすべて完了してから、材料B、C…へと移行する順序になる
• メリット：「材料交換や洗浄の回数を最小限に抑え、作業効率を向上」

「AIのため」だけでなく、「人間のため」にも

Multi-Sigma®は、単に統計的に優れたデータを生成するだけではありません。
「AIのための良質なデータ」を作りながら、同時に「人間が実験しやすいリスト」を提供する。
この両立こそが、私たちならではのこだわりです。

「考える時間」を、もっとクリエイティブなことへ

Multi-Sigma®を使えば、この実験条件の作成を数クリックで実行できます。
「次はどの条件で実験しよう…」と金曜の夕方に悩む時間。
エクセルで乱数を生成して、重複チェックをして、現場のために表を並べ替える単純作業。
もう、その時間は必要ありません。
空いた時間は、データの深い考察に使ってください。
新しい仮説を立てることに使ってください。
チームとのディスカッションに使ってください。
あなたにしかできない、クリエイティブな仕事のために。