次元削減(1) 主成分分析
はじめに
本記事では、次元削減手法について解説します。今回は、主成分分析と呼ばれる手法を用いて次元削減を行う方法をご紹介します。この記事では、パラメータ選択ではなく、元々のパラメータ数よりも少ない数の新しいパラメータを作り、その新しいパラメータが張る低次元空間でデータを表現することを次元削減と呼んでいます。
機械学習を用いたデータ分析で、なぜ次元削減が必要になるのでしょうか？
一般に、説明変数のパラメータ数が多い（高次元）データをそのまま取り扱うと、さまざまな問題が発生する可能性があります。その1つとして考えられることは可視化による直感的な理解が難しい点があります。例えば、6次元のデータの場合はデータをそのまま可視化することは困難です。このような場合、6次元データを任意の2つのパラメータ軸に正射影して描画する事が多いですが、この方法では、必ずしもデータの分布全体を直感的に把握できるとは限りません（図1左図参照）。こういった場合に、それらデータを次元削減し2次元や3次元のデータに変換できれば、可視化によって次元削減された低次元空間内での分布については直感的な理解が得られるかもしれません（図1右図参照）。図1の事例では、6次元データを任意の2次元に射映したプロットではデータの特徴を掴むことは難しいですが、ある手法によりデータを2次元に次元削減すると、直感的にはデータが2つのクラスターに分かれているように見受けられます。このように、データの可視化とその理解のためにも次元削減が用いられることが多いです。この図1でどのような手法によって次元削減を行ったのかについては、本記事で後ほどご説明します。
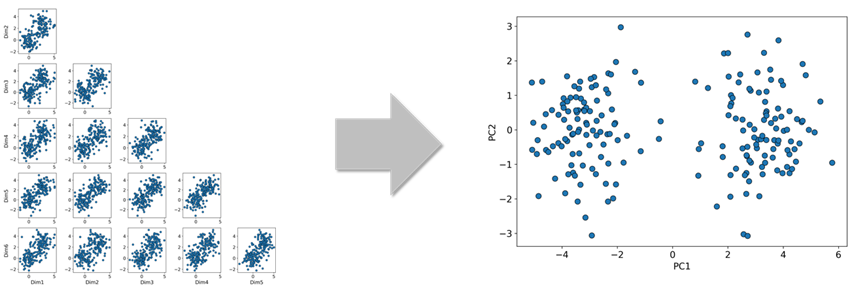
図1：6次元元データを2次元に射影したプロット
また、次元数と比較してデータ数が限られている場合も問題となりうるケースがあります。例えば、100次元といった高次元空間にデータが20点しかない場合、これらデータ点は疎に存在している状況となり、機械学習のモデルを構築するときに疎なデータに過剰に適合してしまう可能性もあります。そのような状況では、高次元空間内の未知のデータに対する予測精度は低くなリます。それらの高次元データを次元削減によって低次元空間に射影し、低次元空間でのデータ分布を推測するに十分なデータの数があれば、射影された低次元空間での予測精度は改善するかもしれません（図2参照）。この時に用いた次元削減手法についても後述します。
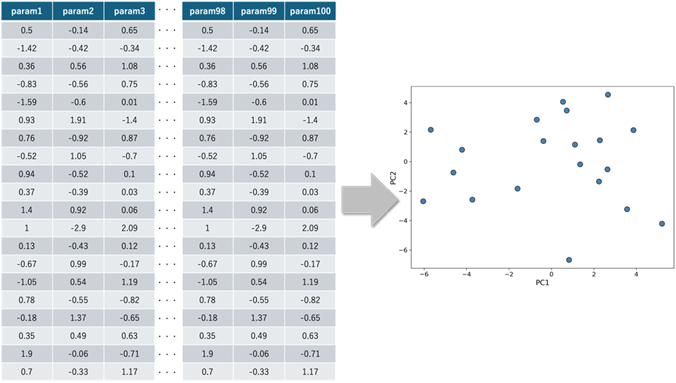
図２：100次元20点のデータ（表）と2次元に次元削減したプロット（図）
さらに、高次元データの場合、データに含まれるパラメータ数が膨大なため、演算処理に必要な計算資源が大幅に増加し、計算負荷が非常に大きくなることが問題です。次元削減を行うことで、高次元データを低次元データに変換することで、計算にかかる負荷を低減させ、全体の処理時間や学習時間を短縮することが可能になります。
主成分分析
では、どのような次元削減手法を用いて高次元データを低次元データに変換すれば良いのでしょうか。
次元削減に用いることができる手法は多数存在します。有名な手法では、主成分分析、独立成分分析、t-SNE（t-Distributed Stochastic Neighbor Embedding）、オートエンコーダ、ランダムプロジェクション、カーネル主成分分析、などが挙げられますが、本記事では主成分分析について解説します。
主成分分析とは、データの次元削減を行う時に、データのばらつき（分散）を基準にして、低次元空間にデータを射影する手法です。具体的なイメージを掴むために、下記の図3に、主成分分析を用いて2次元データを1次元に射影した例を示しています。
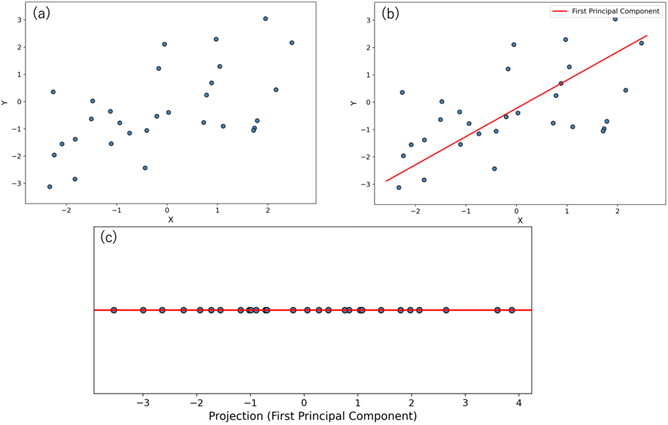
図3：(a)2次元に分布しているデータのプロット、(b)2次元データに対して主成分分析を行い第一主成分方向（赤い斜線）を示したプロット、(c)元の2次元データを主成分方向に射影したプロット。
図3(b)では、赤色の斜線で示された新しい軸は元の2次元データのうち最もばらつきが大きくなる軸を示しています。最もばらつきが大きくなるこの軸方向の基底ベクトルを第一主成分と呼びます。図3(c)からわかるように、第一主成分方向の軸に射影されたデータは、元のデータのx軸やy軸に射影されたデータと比べると、ばらつきが大きくなっています。ばらつきを基準にする理由は、データがばらついているほどデータ間の違いを見分けやすくなるため、データの情報が多いと考えるからです。
元のデータは2次元データなので、第一主成分方向の軸に射影したデータだけでは元のデータを完全に表すことはできません。そこで、第二主成分を考えるのであれば、第一主成分に直交する方向の中から最もばらつきを大きくするベクトルを選びます。元データが2次元の場合は、第一主成分の軸に直交する軸は1つしかありませんので、一意に定まります。
同様に、高次元空間のデータに対しても、第一主成分、第二主成分、第三主成分・・・の軸を求める事ができます。では、高次元空間から低次元空間へデータを射影する時に、どのくらいまで次元削減をすれば良いのでしょうか。その疑問に対する答えの1つとして累積寄与度という概念があります。
このように主成分分析では、ばらつきの大きくなる方向に主成分をとります。そして、元のデータをそれら主成分方向に射影した値を主成分得点と呼んでいます。これらの主成分得点を用いてデータを表現することで、次元削減ができる仕組みになっています。
寄与度・累積寄与度
主成分分析はデータのばらつきに注目して新しい軸方向（主成分）を決定し、元のデータを主成分方向に射影することで、次元削減を行う手法でした。この場合、高次元からどの程度の低次元空間に次元削減することが一般的なのでしょうか。
この問いに答えるためには、主成分分析における寄与度、という概念を用いることが一般的です。寄与度とは、各主成分がデータ全体のばらつきをどの程度を説明できているかを表す指標です。例えば、第一主成分の寄与度が45%であった場合、第一主成分方向に射影されたデータだけで、データ全体のばらつきの45%が表されていることになります。主成分分析の手続きでは、各種成分に対して寄与度を算出することができますので、第一主成分から第n主成分までの累積された寄与度を計算することもできます。このようにして積み上げていった寄与度を累積寄与度と呼びます。この累積寄与度を用いて、例えば、元のデータのばらつきの95%が説明できる、主成分m主成分までを使用するといったように判断を下すことが多いです。
主成分得点と主成分負荷量
主成分分析では、主成分得点と主成分負荷量という用語を用いて表現される概念があります。主成分分析に関する分析を理解するために、これらの用語についても解説します。
主成分得点
主成分得点とは、元のデータを主成分方向に射影した値として定義されます。元の空間のデータを第一主成分の方向に射影した時には、各データ点と第一主成分ベクトルとの内積を計算することで、第一主成分軸に射影した値を得ることができます。内積によって得られるこの値が、そのデータの第一主成分得点となります。例えば、4次元空間で、第一主成分ベクトルが
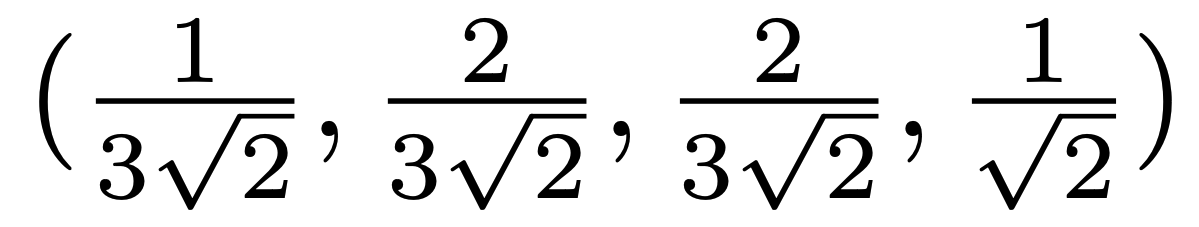
である時に、データ点（2, 3, 5, 1）Tと第一主成分ベクトルから、主成分得点は下記の式1のように計算されます。
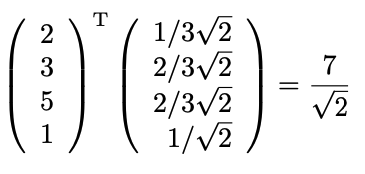
式1：主成分得点の計算
主成分負荷量
主成分負荷量とは、次元削減をする前のデータの空間の各軸が、主成分に対してどの程度寄与しているのかを表した値として定義されます。例えば、10次元のデータに対して主成分分析を用いて次元削減を行い、第一主成分が求められたとします。この時、第一主成分ベクトル（v_{1,1}, …, v_{1,10}）の各要素は、それぞれ元の空間の各軸がどの程度第一主成分ベクトルに寄与しているかを表しているものになります。
主成分分析における標準化
これまでの主成分分析の説明においては、データの前処理については言及していませんでした。元の空間のデータをそのまま利用して、主成分分析を行った場合の事例を説明してきましたが、多くのデータ分析事例では、データの前処理として元のデータに対して標準化を行うことが多いです。それでは、なぜデータの前処理として標準化を行うことが多いのでしょうか。
標準化という処理は、各パラメータの単位の違いなどによる影響を除外するために、データを変換する手法です。例えば、X1という変数のデータに対して、変数X1の平均値と標準偏差を計算し、 変数X1の各データから平均値を引いて標準偏差で割った値を計算します。これが変数X1に対する標準化の手続きです。他の変数についても同様の計算を行います。この前処理により、各変数は平均0で分散1の分布に変換されたことになります。
例えば立方体の縦方向をcm単位で、横方向をmm単位で、高さ方向をm単位で表示していると、それらの数値だけをそのまま扱っても実際の大きさを適切に表現することはできません。また、主成分分析では各変数のばらつきが大きな意味を持ちますが、単位を考慮せずに数値だけで判断すると、上記の例ではmm単位で表されている横方向の分散の値が大きくなってしまいます。一方で、これらのデータを標準化によって変換すると、それぞれの変数（縦方向、横方向、高さ方向）は、平均0、分散1のデータになります。これにより、各軸方向のばらつきは均一になりますので、主成分分析を適用する際には変数間の相関に着目することになり、データの内部構造を適切に評価しやすくなると考えられます。
Multi-Sigmaにおける主成分分析
Multi-Sigmaでは、高次元データを取り扱う際に、次元削減をするための手法として主成分分析を導入する予定です。Multi-Sigmaでは、説明変数は200種類まで取り扱うことができますが、主成分分析により次元削減を行うことで、より高次元のデータも取り扱えるようになります。また、説明変数の次元が200以下であっても、主成分分析を利用することでデータ構造を捉えやすくなることもあります。Multi-Sigmaでは主成分分析の実行も、ノーコードで誰にでも利用できるようになる予定です。
